Амортизаторы

По статическим и динамическим исследованиям и расчетам амортизационных устройств имеется немало сообщений. Однако лишь в немногих уделяется внимание оценке механических свойств резиновых конструкций по связи с составом резиновых смесей и технологическими особенностями производства. В расчетах конструкций, следуя принципу суперпозиции, авторы принимают зависимость напряжений / и деформаций е резины линейной, а поэтому и ограничиваются теми пределами деформаций, в которых считают возможным это допущение. Особенности свойств резины в больших деформациях и перемещениях освещают В. Л. Бидер-ман и Э. Э. Лавенделл. В литературе приводятся некоторые материалы предлагавшихся расчетов.
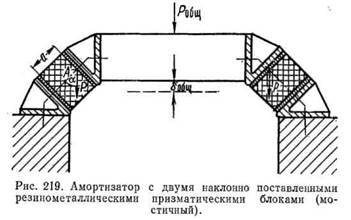
Мостичный амортизатор. Исследование статических свойств мостичного амортизатора, состоящего из двух наклонно поставленных призматических резиновых блоков, прочно привулканизо-ванных к металлической арматуре, и работающего в сдвиге и сжатии (рис. 219), приводит Гебель. Вследствие прочного мостичного соединения направление деформации ббщ не произвольное, а идентично с направлением силы
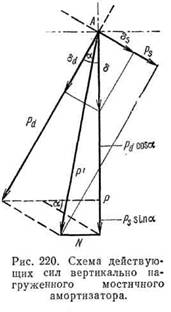
Относительная жесткость каждого амортизатора с = Я/ббЩ; общая относительная жесткость системы С = 2Р/ббщ-Вынужденное поведение амортизатора является следствием горизонтальной силы N (рис. 220), возникающей в результате прочного соединения обоих наклонно поставленных блоков. Результирующая для Р и N сила Р’ одновременно является таковой же для усилия сдвига Рсд и усилия сжатия Рст. Из соответствующих деформаций сдвига бсд и сжатия беж следует общая деформация (осадка) ббщ амортизатора при нагрузке. Величина ббщ меняется, как и ее компоненты, с изменением угла а — наклона оси амортизатора к вертикали. Приняв Л за начальную точку приложения силы Р, применяем следующие уравнения:
а) Установление усилия Рсд, определяющего «чистое» напряжение сдвига. Следуя обозначениям главы 8 и принятым здесь, получаем:
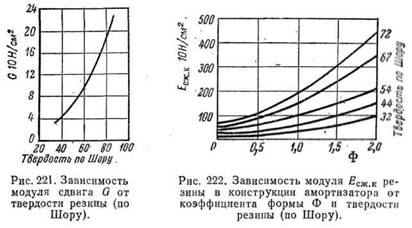
Модуль сдвига резины и 1 ебель принимает в графической зависимости от твердости, но не зависящим от формы резины и конструкции блока (рис. 221).
При а не выше 20° тангенс угла практически можно принять равным дуге, следовательно
б) Установление усилия Рст, определяющего «чистое» напряжение сжатия. Принимая зависимость напряжения / от деформации е линейной, имеем:
Модуль продольной упругости Еож.я конструкционно связан ной резины, привулканизованной к металлическим пластинам, IV бель принимает в графической зависимости от коэффициент,! формы Ф и от твердости резины (рис. 222).
в) Определение общего прогиба двух наклонно поставленных блоков амортизатора. Из уравнений (13.32), (13.36) и (13.37) для рассматриваемого случая
Из уравнения (13.38) можно вычислить ббщ для различных углов а или по заданным значениям бсд и бсж найти предел линейной зависимости Рбщ — бобщ-
Расчет числа собственных колебаний мостичного амортизатора. При расчете числа пс (в Колеб/мим) собственных колебаний системы в вертикальном направлении с массою m применяют уравнение
Поскольку прогибы бобщ связаны с нагрузкой Рбщ через относительную жесткость С, естественно ожидать, что при циклически изменяющейся нагрузке относительная динамическая жесткость
(практически не зависящая от частот, обычных для машин) раз-лична для разных видов резин
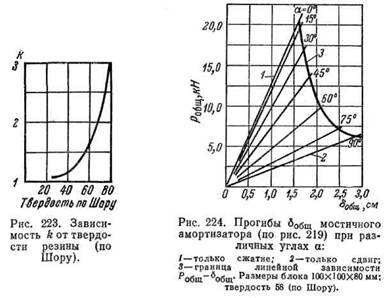
На рис. 223 приведена зависимость коэффициента k от твердости резины.
Масса m вычисляется (приближенно) как
Пример расчета. Требуется.
а) Показать зависимость упругих прогибов бобщ амортизатора (рис. 224)
от Роощ для углов а — 0,15, 30, 45, 60, 75 и 90°, если $ — 10 X 10 см =» 100 см2, толщина резинового слоя а = 8 см, твердость резины по Шору 58, G = 8,4 • • 10 Н/см2 Ф = 0,313 и Есж. и = 52 • 10 Н/см2.
б) Показать зависимость числа собственных колебаний пс амортизатора
для тех же значений углов а и Робщ = 6,0 кН, если k = 1,5 (из графической
зависимости от твердости по рис. 223).
Решение. Применяя уравнение (13.38) и задаваясь значением Робщ, находим бобщ для заданных величин углов. Решение приведено на рис. 224. При а = 0° происходит только сжатие блоков; при а = 90° — только сдвиг; в последнем случае с прогибом, в 6 раз большим, чем в первом. Кривая рис. 224, определяющая границу линейности зависимости Рбщ— 5бщ, вычислена на основании уравнения (13.38) по формуле
На рис. 225 приведена зависимость собственной частоты колебаний от угла а, как сследует из графика, при а =. 0° пс самое высокое, а при а = 90″ (при сдвиге) самое низкое.


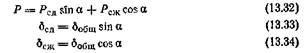
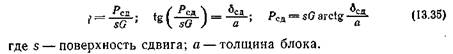


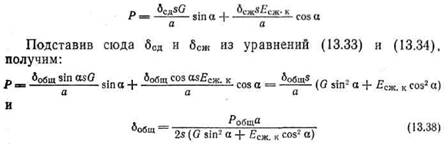

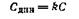
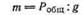
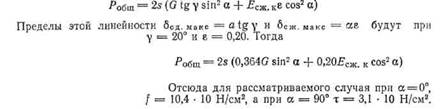

такого рода «расчеты» не могут быть приемлемыми, по следующим причинам:
1. резина — почти с самого начала деформирования имеет существенно нелинейные характеристики, а потому нет никаких аналитических формул, позволяющих определить даже статическое перемещение
даже статические задачи для гиперупругих материалов решаются только численно.
2. теория малых ЛИНЕЙНЫХ — для определения «собственных» частот так же не может быть использована, так как:
а) одно из основных требований ЛИНЕЙНОСТИ изучаемой конструкции — ЛИНЕЙНЫЙ модуль упругости — ПОСТОЯННЫЙ в процессе колебания конструкции = это требование совершенно не выполнимо для конструкций из гиперупругих материалов
б) Деформация конструкций из гиперупругих материалов почти всего геометрически нелинейна — что автоматически исключает применение теории МАЛЫХ ЛИНЕЙНЫХ колебаний.
т.е. можно говорить о существовании «мгновенных» значений собственных частот для конструкции из гиперупругих материалов.
«собственные частоты» колебаний будут меняться в каких-то диапазонах, ЕСЛИ рассматриваемая система ЛИНЕЙНА с точки зрения независимости частот и амплитуд колебаний.
Это МОДЕЛЬНАЯ задача, решена с целью пояснения необходимости использования «реальных» моделей гиперупругих материалов при расчете конструкций из резиноподобных (гиперупругих) материалов.