Как уже отмечено в главе 5, при динамической нагрузке циклического (периодического) или импульсного (ударного) возбуждения возникает необходимость уменьшения действующей силы (статическая плюс динамическая), передаваемой от неуравновешенной машины к фундаменту, или уменьшения амплитуды вынужденных колебаний от вибрирующих корпусов к монтированным на них приборам. Это необходимо для защиты прочности сооружений и в целях снижения производственного шума.
Ниже, например, рассматривается случай использования резиновых плоских амортизационных прокладок, осуществляющих гашение колебаний (демпфирование) за счет свойств, присущих резине (гистерезисных ее потерь и жесткости).
Логарифмический декремент т), представляя собой натуральный логарифм величины отношения двух последовательных амплитуд колебания К и К2, служит показателем затухания за один период. Чем меньше rj, тем лучше изоляция, зависящая по уравнению (13.42) от отношения fB/fcи от логарифмического^ декремента затухания Ф. Уравнение (13.42) для случая/в//с = = 1,41 при всех значениях д дает ц =» 1, т. е. в этом случае амортизирующего действия нет. Если в дальнейшем анализе уравнения (13.42) принять Ф близким к нулю, т. е. считать внутреннее трение в амортизаторе пренебрежимо малым, то получим:
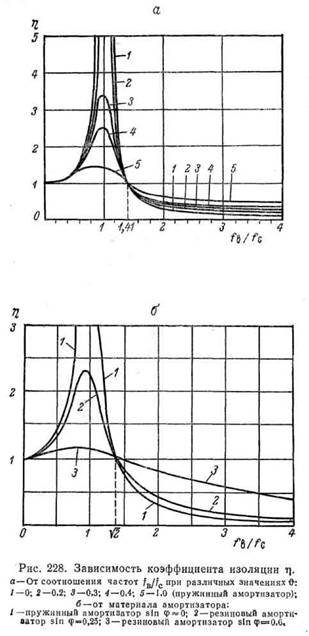
При fB = /с уравнение (13.42′) теоретически приводит к ц = оо, что характеризует состояние резонанса. Резкое возрастание ц в зоне резонанса отвечает такому же увеличению амплитуды колебаний агрегата и силы, передаваемой основанию.
Допущение, положенное в основу уравнения (13.42′), в достаточной мере справедливо для металлических пружинных амортизаторов, не имеющих существенного внутреннего трения и осуществляющих амортизацию за счет приданной металлу формы. Для резин же, применяемых в амортизационных устройствах, величина f}, зависящая от гистерезисных потерь, находится в пределах 0,3—0,8. Таким образом, резиновый амортизатор и при резонансе дает конечную величину ц.
Так как увеличение tj при резонансе не связано с возрастанием энергетических затрат, то в ряде случаев допустимо применение резиновых амортизаторов для работы вблизи резонансной зоны. Это, например, бывает в работе грохотов, сит и других объектов. Но такая работа, именно из-за наличия внутреннего трения в резине, связана со значительным нагревом резинового амортизатора и может вести к преждевременному его износу.
На рис. 228, а приведена зависимость ц от fjfc, следуя величинам логарифмического декремента затухания О. Чем ниже ft, тем выше значение ц в резонансной зоне. Одновременно, однако’ ц уменьшается с увеличением отношения fjfc. При этом чем выше &, тем более пологий, ближе к х| = 1, ход кривой зависимости
Так как О зависит от гистерезисных потерь в резине, а последние определяются синусом угла сдвига фаз между силой быть заменено sin2 cp. Sin ф —легко определяемая экспериментом характеристика резины.
Как уже отмечено, для получения хорошей изоляции необходимо, чтобы частота fcбыла меньше, чем частота /в. Так как fможет быть выражена через вес Р, осадку 6 и ускорение силы тяжести gпо уравнению
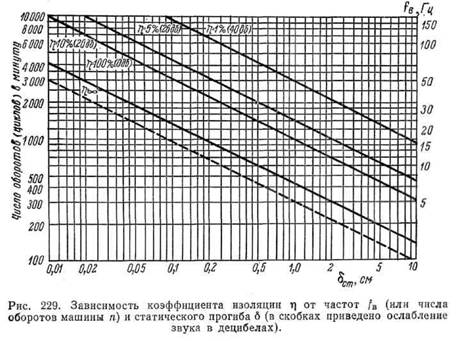
Таким образом, если известна осадка б резиновой прокладки под заданной статической нагрузкой Р, определяемой весом агрегата, то может быть найдена собственная частота /с (без затухания) системы агрегат —амортизатор; fcбудет тем меньше, чем больше б. Осадка б = /ге будет тем значительнее, чем ниже модуль резины и чем меньше коэффициент формы резиновой прокладки. Однако применение резиновых прокладок с 1гсвыше 3—5 см не рекомендуется, так как это приводило бы к возможности боковых смещений агрегата. Для подбора бсм, в зависимости от требуемого т) и заданного /в (или п), предложен график* (рис. 229) с линейной зависимостью / — бсм. Нижняя
кривая, помеченная т] « оо, отвечает /в = fo» т. е. состоянию резонанса.
На рис. 229 приняты б статические, отвечающие статическому режиму деформации и статической жесткости. Так как динамическая жесткость, зависящая от динамического модуля, выше статической, то для расчетов амортизаторов прогибы должны быть взяты меньшими. В качестве поправочного множителя можно применять величины /г-1, коэффициента, приведенного на рис. 223, или
отношение модулей Ест/Етп по данным, приведенным в главе 8. Но можно также, не меняя величины 6, в дальнейшие расчеты вводить значение £дин.сж.к. В ответственных случаях величины Яднн.сж.к следует находить экспериментально. Коэффициент изоляции ц считают практически достаточным в пределах 0,2—0,5.
Задавшись допустимым напряжением /сж резиновых прокладок, находят их высоту h, отвечающую требуемой зависимости Р — б, применяя уравнение:
Допустимое напряжение /Сж для амортизационных упругих прокладок дано в табл. 31.
По найденному fCmопределяют площадь sи размеры прокладок.
Пример расчета. Рассчитать упругую прокладку под машину, работающую при 3000 об/мин. Вес машины 6,0 кН, вес фундаментной плиты 4,0 кН.
Принимаем отношение fB/fc = 3, что дает /с= 6Q^ = 17 Гц. Из рис. 229
находим, что частота собственных (или резонансных) колебаний /с = 17 Гц (1000 колеб/мин) соответствует прогибу б = 0,1 см.
Выбрав в качестве прокладок резиновые плиты с отверстиями с Еюш. еж. к = = 40-10 U/cu2и принимая допустимую нагрузку /сж = 1-10 Н/см2, находим высоту прокладки h
При /о = 17 Гц вибрация, передаваемая фундаменту, будет ослабляться для всех частот, начиная с частоты f= -/2fc= 24 Гц.
Если принять число прокладок равным 6, то размеры каждой могут быть, например, 10 X 16,7 см или же d— 14,6 см. В более точном расчете следует принимать во внимание уменьшение общей жесткости прокладок с увеличением числа их, вследствие изменения коэффициента формы Ф [см. уравнение (8.16)].
Схему детального прикладного вибрационного расчета резино-металлических амортизаторов приводит Б. М. Горелик. Элементы теории резонансных грохотов исследует В. Н. Потураев . Расчеты опор и шарниров в мостах дает Л. И. Мещеряков.



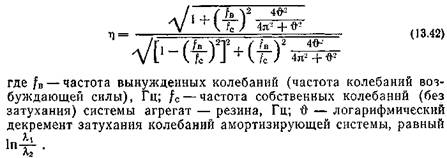

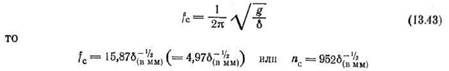


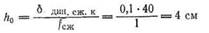
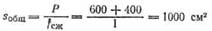
Теория малых линейных колебаний почти никогда не может быть применена к гиперупругим материалам.
Такого рода «расчеты» практиковались лет 50-60 назад, когда у инженеров ничего кроме логарифмической линейки не было.
В настоящее время — у любого инженера есть персональный компьютер и МКЭ программы.